Hampir setiap hari kita melihat Matahari terbit dan tenggelam, kecuali pada saat langit sedang mendung. Seberapa jauh sih Matahari dari Bumi? Mungkin itu yang membuat kamu bertanya-tanya ya. Jawaban yang paling singkat adalah 1 AU (Astronomical Unit).
Orang yang pertama kali mencoba menghitung jarak Matahari dari Bumi secara kasar adalah Aristarchus, sekitar 2.250 tahun yang lalu, dengan menggunakan trigonometri ini pelajaran waktu SMP
Orang yang pertama kali mencoba menghitung jarak Matahari dari Bumi secara kasar adalah Aristarchus, sekitar 2.250 tahun yang lalu, dengan menggunakan trigonometri ini pelajaran waktu SMP
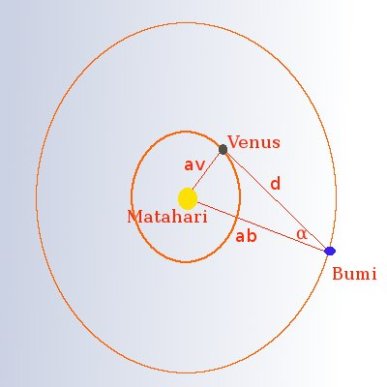
Belakangan, tepatnya pada tahun 1653, seorang astronom bernama Christiaan Huygens menghitung lagi jarak Matahari dari Bumi dengan teliti, dengan menggunakan metode triangulasi yang melibatkan Matahari, Bumi dan Venus. Hasil perhitungan Huygens dikoreksi lagi oleh Giovanni Cassini pada tahun 1672, dengan menggunakan metode paralaks, yang memuat perhitungan sudut secara lebih teliti.
Bagaimana sebenarnya cara astronom untuk dapat menghitung dan mengetahui jarak diantara benda-benda langit seperti Matahari, planet, bintang, galaksi dan sebagainya. Metode penentuan jarak bintang dan objek luar angkasa lainnya yang paling sederhana adalah metode paralaks trigonometri. Akibat perputaran Bumi mengitari Matahari, maka bintang-bintang yang dekat tampak bergeser letaknya terhadap latar belakang bintang-bintang yang jauh. Dengan mengukur sudut pergeseran itu (disebut sudut paralaks), dan karena kita tahu jarak Bumi ke Matahari, maka jarak bintang dapat ditentukan.
Pada abad ke-19 dilakukan pengukuran jarak bintang dengan cara Paralaks Trigonometri. Untuk memahami cara ini, lihatlah gambar berikut ini.

Akibat pergerakan Bumi mengelilingi Matahari, bintang terlihat seolah-olah bergerak dalam lintasan elips yg disebut elips paralaktik. Sudut yg dibentuk antara Bumi-bintang-Matahari (p) disebut paralaks bintang. Makin jauh jarak bintang dengan Bumi maka makin kecil pula paralaksnya. Dengan mengetahui besar paralaks bintang tsb, kita dapat menentukan jarak bintang dari hubungan:
tan p = R/d
R adalah jarak Bumi – Matahari, dan d adalah jarak Matahari – bintang. Karena sudut theta sangat kecil persamaan di atas dpt ditulis menjadi
Ø= R/d
pada persamaan di atas p dlm radian. Sebagian besar sudut p yg diperoleh dari pengamatan dlm satuan detik busur (lambang detik busur = {”}) (1 derajat = 3600″, 1 radian = 206265″).
Oleh krn itu bila p dalam detik busur, maka
p = 206265 (R/d)
Bila kita definisikan jarak dalam satuan astronomi (SA) (1 SA = 150 juta km), maka
p = 206265/d
Dalam astronomi, satuan jarak untuk bintang biasanya digunakan satuan parsec (pc) yg didefinisi sebagai jarak bintang yg paralaksnya satu detik busur. Dengan begini, kita dapatkan
1 pc = 206265 SA = 3,086 x 10^18 cm = 3,26 tahun cahaya
p = 1/d –> p dlm detik busur, dan d dlm parsec.
Dari pengamatan diperoleh bintang yg memiliki paralaks terbesar adalah bintang Proxima Centauri yaitu sebesar 0″,76.
Dengan menggunakan persamaan di atas maka jarak bintang ini dari Matahari (yg berarti jarak bintang dgn Bumi) adalah 1,3 pc = 4,01 x 10^13 km = 4,2 tahun cahaya (yang berarti cahaya yg dipancarkan oleh bintang ini membutuhkan waktu 4,2 tahun untuk sampai ke Bumi).
Sebarapa jauhkah jarak tersebut??
Bila kita kecilkan jarak Bumi – Matahari (150 juta km) menjadi 1 meter, maka jarak Matahari ke Proxima Centauri menjadi 260 km ,Karena sebab inilah bintang hanya terlihat sebagai titik cahaya walau menggunakan teleskop terbesar di observatorium Bosscha.
Sebenarnya ada beberapa cara lain untuk mengukur jarak bintang, seperti paralaks fotometri yg menggunakan kuat cahaya sebenarnya dari bintang. Kemudian cara paralaks trigonometri ini hanya bisa digunakan untuk bintang hingga jarak 200 pc saja. Untuk bintang2 yg lebih jauh, jaraknya dapat ditentukan dengan mengukur kecepatan bintang tersebut.
Perhitungan jarak bumi ke matahari ini didasarkan pada perhitungan kecepatan cahaya matahari sampai ke bumi dengan kecepatan rata-rata sekitar 8,3 menit.
keterlambatan ini bisa dihitung dari panjang gelombang sinar matahari yaitu ultra-violet yang bergeser beberapa nanometer dari panjang gelombang yang dihasilkan oleh proses termonuklir
kita tahu bahwa cahaya matahari terlambat 8.3 menit* dan kecepatan cahaya adalah 3x10^8 m/s sehingga jarak tempuhnya adalah:
Jarak Matahari = 8.3 x 60 x 3x10^8 m
Jarak Matahari = 149 000 000 km
Jadi jangan beranggapan Jika Ilmuwan cuma ngasal dalam perhitungan karena ditinjau dari namanya mereka pasti orang ber-Ilmu.


